A Raytracer in Python - Part 5 - Non-planar Samplers
In this post we are going to describe and implement non-planar samplers. In the previous post about samplers we implemented and characterized different planar samplers to make antialiasing possible. The characteristic of these samplers was to produce regular or random points on a plane with x,y between zero and one. To implement effects such as simulation of lenses behavior, reflections and so on, we also need to be able to shoot rays according to geometrical patterns other than the plane. More specifically, we need to be able to map points on a disk (to simulate lenses) or on a hemisphere (to simulate other optical effects such as reflections), while at the same time preserving the good characteristics of the random distributions outlined in the planar case.
To achieve this, the samplers now implement two new methods, BaseSampler.map_samples_to_disk() and BaseSampler.map_sampler_to_hemisphere(). They are in charge of remapping the planar distribution to a disk or to a hemisphere, but with a couple of twists: in the disk remap, the points in the range [0:1] must be remapped to a full circle from [-1:1] in both axes, so to cover the circle completely while preserving the distribution. This is done through a formulation called Shirley's concentric maps.
In the hemisphere remapping, we also want to introduce a variation in the density so that it changes with the cosine of the polar angle from the top of the hemisphere. In other words, we want an adjustable parameter e to focus the point density closer to the top of the hemisphere.
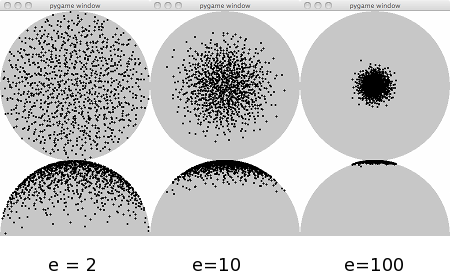
We will need the characteristics of this distributions later on, when we will have to implement reflections and other optical effects. As you can see from the above plot, higher values of the parameter e produce a higher concentration of the points close to the top of the hemisphere. On the other hand, a low e parameter tend to produce a more uniform distribution over the full hemisphere.
To obtain the points, the sampler object has now three methods to request an iterator. We are no longer iterating on the object itself, because we need to provide three different iteration strategies. Methods BaseSampler.diskiter(), BaseSampler.hemisphereiter() and BaseSampler.squareiter(), each returning a generator over the proper set of points. Note that the hemisphere point generator returns 3D points, differently from the other two returning 2D points.